This guide acts as a follow-up to the talk Binary vs Interpolation Search.

Time complexity and search algorithms. A walk through their definition, purpose, use cases and constraints. A search algorithm is a technique used to locate an item in a certain data structure.

Introduction

A search algorithm is a technique used to locate an item in a certain data structure.

Before we begin, you should have an understanding of the below:

• Arrays
• Iteration and recursion

Let's give an overview of time complexity and what it entails.

Time Complexity

A way to show how the runtime of a function increases.

Broadly speaking, the time complexity of a program is grouped into three:

• Linear time
• Constant time
• Quadratic time

Linear Time O(n)

The processing time of a program will increase as the size of the input increases.

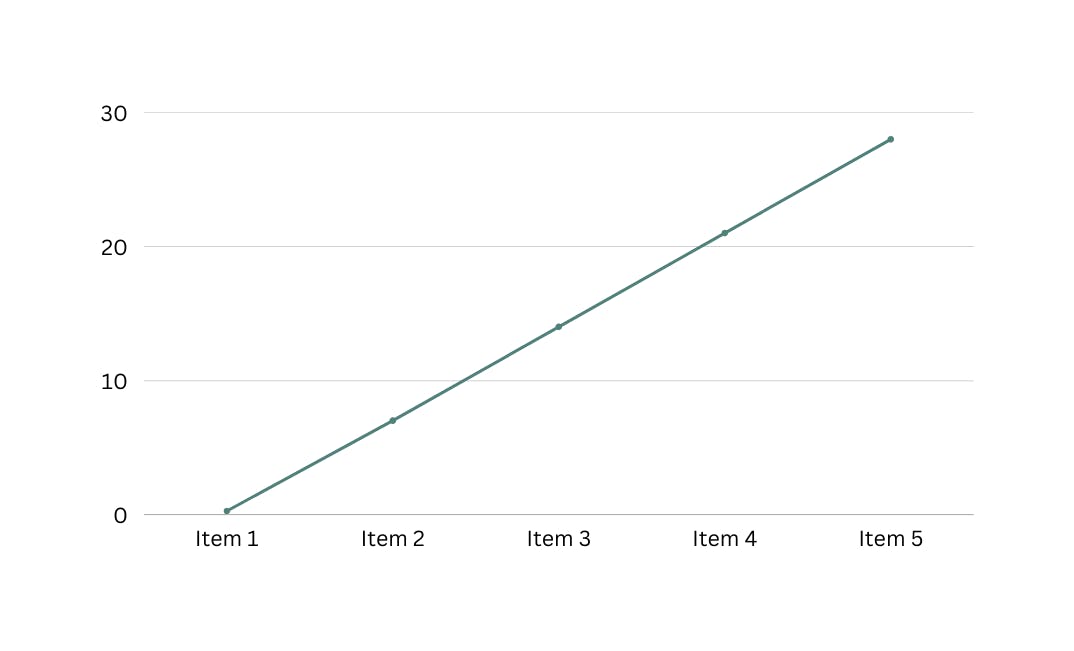
Example We can create a program that processes a list of items stored in an array. A case example can be a program to process locally stored files.

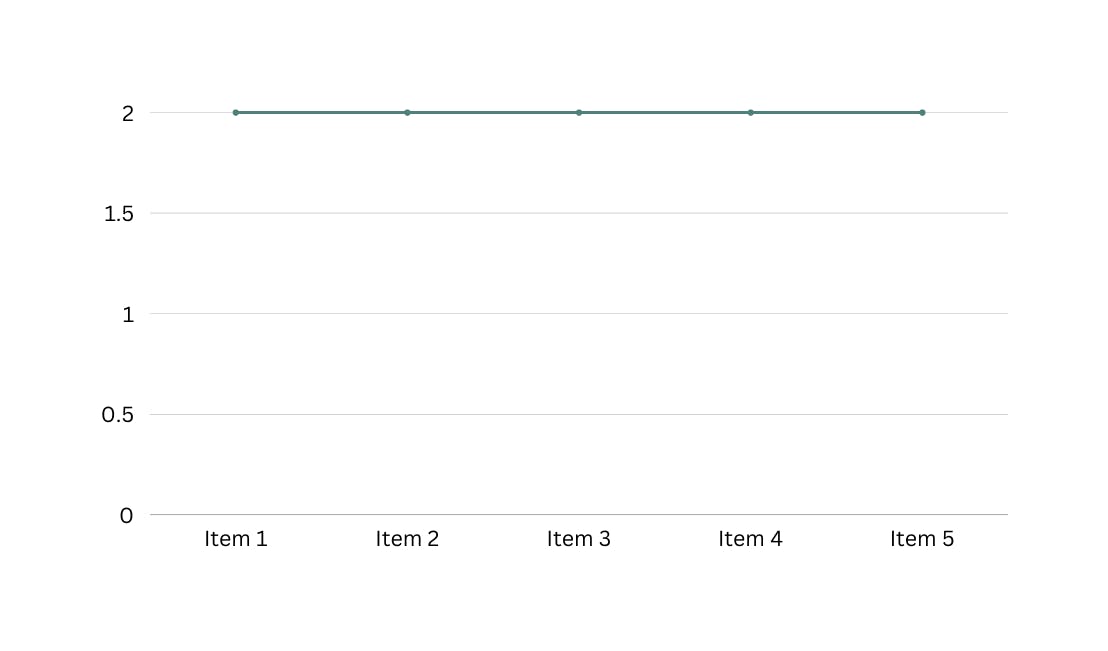
Constant Time O(1)

Here, no matter what input we parse to our program, we get the results in the same time frame. Hence, a process taking 10_000_000 items returns in the same time as the one taking in 7 items.

Quadratic time O(n2)

Where n2 is n squared. As the name suggests, a program will return results in a time period that resembles a quadratic curve. This time is common with multi-dimensional arrays/lists of lists, since:

• We loop over the list(say A) to get individual lists
• We loop over a specific list(say B) in this list to get the item and perform an operation on it.

For reference, the equation:

a + bx + c

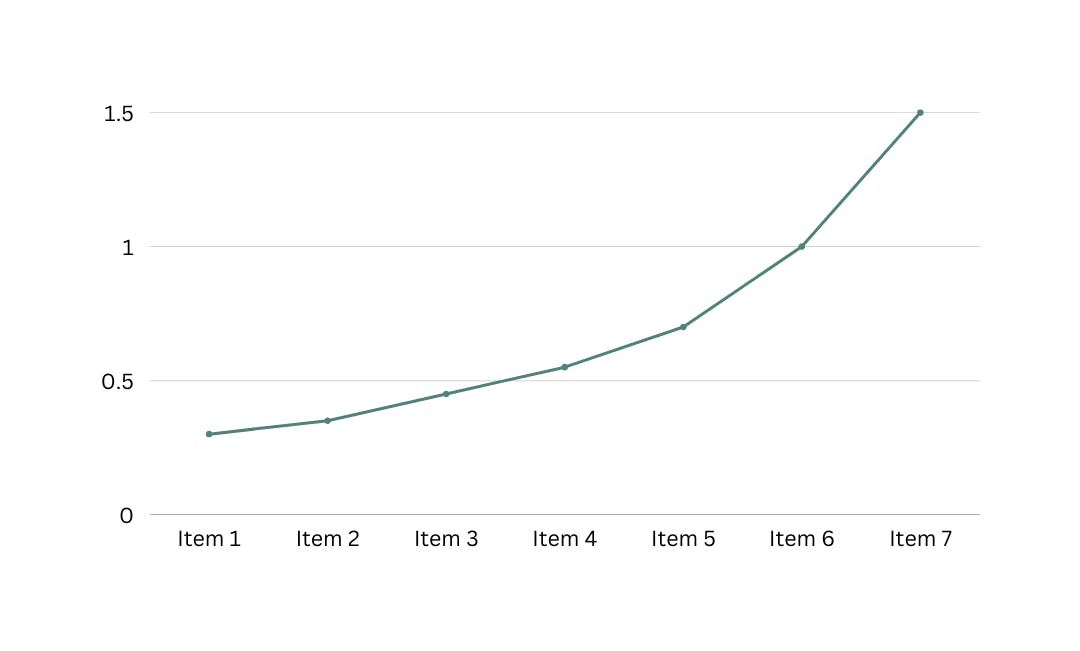
Example: A program to calculate the product of integers in an array.

int array_products(int[] a){
    int product = 0; // O(1)
    for(int number: a){
       product = product * number; // O(1)
   }
return product; // O(1)
}

We can get an overview of how long a function will take, based on how large of an array we have in this particular function/ method.

In our case, since we can get the time complexity of this function as below:

O(1) + n * O(1) + O(1)

Since we are adding a value to the summation x number of times, we have O(1) happening for each of those occurrences. Thus n O(1)*.

Since a constant + another constant is still a constant.

O(1) + n * O(1)

Get the fastest-growing term from the equation, i.e:

n * O(1)

Then remove the coefficient to get O(n) (linear time i.e, the function takes longer to complete the larger the array)

Binary Search

Given a sorted array, binary search locates an item in question, using the 'divide and conquor'

Time complexity: O(log n)

Binary Search pseudocode

1. Get the first and last item of the sorted array.
2. Add the first and last item indexes and divide by 2
3. Get the element in the middle from the step above i.e middle
4. If the value at the middle index is equal to the searched item, return the index
5. If the value at the index is greater than the searched item, set the middle item to be the new high and discard the right
6. If the value at the index is less than searched item, make the item the new low and discard the left side
7. Repeat the process until the index is obtained
8. Return -1 if the item is absent

Visual representation

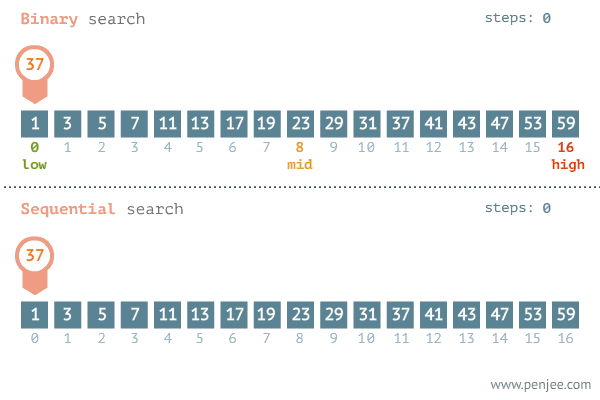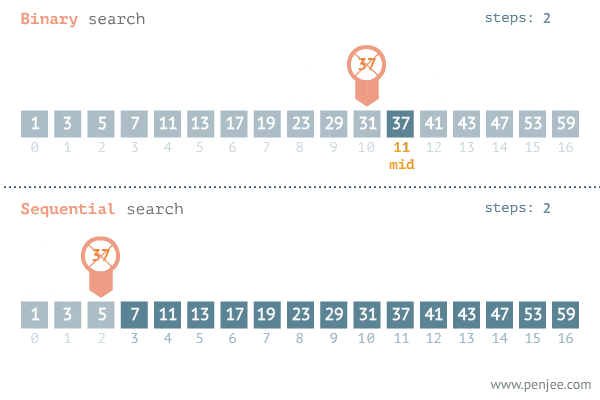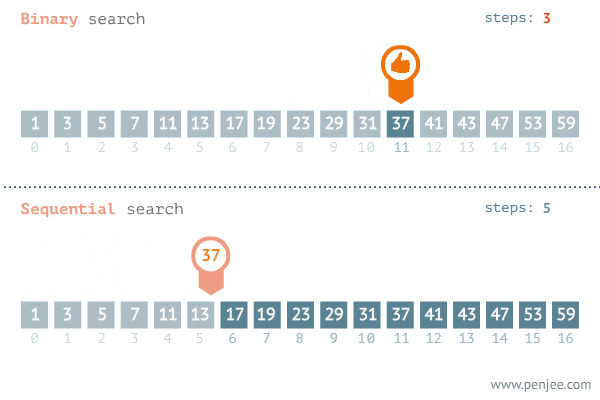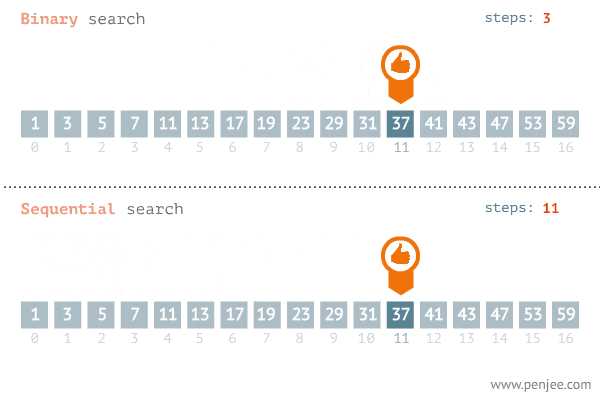
Implementation of binary search

int search( int[] a, target){
    int arrayLength = a.length;
    int left = 0;
    int right = a.length;

    while(left <= right){ 
       int middle = (left + right) / 2;

       if(a[middle] == target){ 
          return middle;
        }

       if(target < a[middle]){
             right = middle - 1;
        }else{
         left = middle + 1;
    }

  return -1;
}

Applications of Binary Search

1. Database indexing

Within your database of choice, a binary tree will be used where it will precompute the middle point on each step, until reaching the single item. More details of database indexing can be found here

1. 3D games and applications.

Binary space partitioning occurs as space is divided into a tree structure and a binary search is used to retrieve which subdivisions to display according to a 3D position and camera.

1. Git debugging with git bisect

2. Autocomplete search

Consider a user typing in a URL on a browser. Given a history of searches, instead of going through each one and comparing, a binary search is used to perform a faster lookup across the history.

1. Searching for prefixes

Instead of an array of integers, you can have an array of strings where you intend to search for an item that starts with a certain string or character sequence.

1. Going through a dictionary to find a word

2. Git cherry picking

A clever example of where this is used is by Sarv Shakti, who used it to identify what commit broke the application

Example: Consider a scenario where you have a list of maps storing student records in your classroom. Given a name, or phone number, which algorithm would you use to search through this? What if the records got to 10_000 or more? How would this grow?

---

Interpolation Search

This is an improvement over binary search. Gets an element from where it is more likely to exist.

Time complexity: O(log log N)

Constraints of interpolation search

1. The array should be sorted
2. The array should be uniformly distributed.

Note: Uniform distribution in an array implies that the difference between subsequent elements should be relatively equal. In this case, an array [10, 30, 300000, 23_000_000] would fail to meet this condition.

Example: Searching for the word 'zelda' in a dictionary of words from letters 'a' to 'z'.

Instead of starting from the middle item in the array, we go closer to the end of the array.

Time complexity and its relation to interpolation search

A walk through the equations

y = m*x + c

arr[index] = m*index + c

where: index: the position of the element in the array arr[index]: the value at this index in the array

arr[low] = m*low + c —– (1)

arr[high] = m*high + c —– (2)

Subtract equation (1) from (2), and we get

arr[high] – arr[low] = m * (high – low)

m = (arr[high] – arr[low]) / (high – low) —– (3)

Say we are searching for an element, K in this array.

arr[index] = m*index + c

Then replacing target in the above equation, we get

target = m*index + c —– (4)

target – arr[low] = m * (index – low)

index – low = (target – arr[low]) / m

index = low + (target – arr[low]) / m

index = low + (target - arr[low])*(high - low) / (arr[high] - arr[low])

Example

Array to search through:

[32, 35, 37, 39, 42, 44, 46, 48]

We will search for target = 42 in the above array.

The size of the array is 8.

low = 0,

high = 7,

arr[low] = 32,

arr[high] = 48

index = 0 + (42 - 32) * (7 - 0) / (48 - 22) = 2.6923 ~ 2

arr[2] = 37 < 42

Remember to floor the value of the index

Interpolation search pseudocode

1. Calculate the Index using the interpolation index formula.
2. If the target is smaller than the item at that index, search in the lower sub-list. Calculate the index for the left sub-array. Let low = index - 1
3. If the target is greater than the item at that index, search in higher sub-list. Calculate the position of the right sub-array by assigning low = index + 1.
4. If the target is a match, return the index of the item from the array and exit.
5. If it is not a match, probe position.
6. Repeat until the match or array is eventually 0

Implementation of Interpolation search

int search(int[] array, int target) {
    int n = array.length;
    int low = 0;
    int high = n - 1;

    while (low <= high) {

        int index = low + ((target - array[low]) * (high - low)) / (array[high] - array[low]);

        if (array[index] < target) {
            low = index + 1;
        } else if (array[index] > target) {
            high = index - 1;
        } else {

            return index;
        }
    }

    return -1;
}

Applications of interpolation search

Interpolation search can be used in the same areas where binary search is used. The only caveat is that this data must be uniformly distributed. A failure to meet this condition will give you a time complexity of O(n).

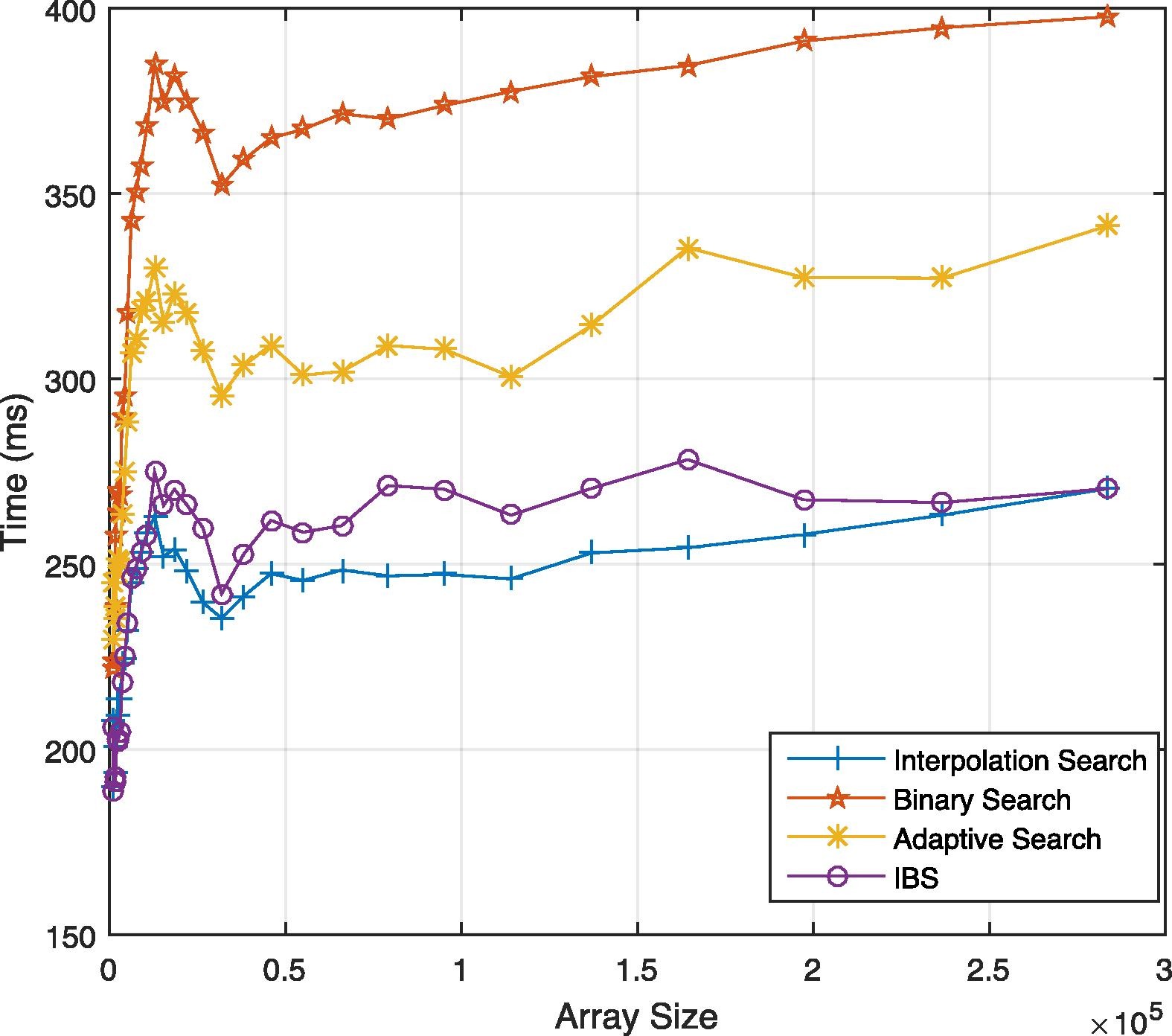
Benchmark

Comparatively, given uniformly distributed data, this difference might occur as below:

Resources and questions

These are locations to practice your data structures along with links to various challenges that may hold the above mentioned concepts or pivot them accordingly.

• Leetcode
• Exercism
• Hackerrank
• Algoexpert

• The two sum problem
• How many numbers are smaller than the current number
• Middle of a linked list
• Container with most water
• OpenSource collection - TheAlgorithmCore

Other types of search algorithms

• Linear search / sequential search
• Breadth-first search
• Depth-first search
• Jump search
• Exponential search
• Fibonacci Search

Conclusion

There are more search algorithms out there. This is by no means a comprehensive list, and by no means are you expected to know all of them. A single algorithm can be used as the basis for other searches. With that said, there is no silver bullet. You choose what works based on the constraints at hand.

References:

Mohammed, A. S., Amrahov, Ş. E., & Çelebi, F. V. (2021). Interpolated binary search: An efficient hybrid search algorithm on ordered datasets. Engineering Science and Technology, an International Journal, 24(5), 1072–1079. doi.org/10.1016/j.jestch.2021.02.009

Manolopoulos, Y., Theodoridis, Y., & Tsotras, V. (2012). Advanced Database Indexing. In Google Books. Springer Science & Business Media. books.google.com/books?hl=en&lr=&id..

Originally published at marvinkweyu.net/talks/binary_vs_interpolati..